Calculation of anisotropic superconductivity#

Author: S. Mishra (v1.1, 06/01/2024) Revision: S. Mishra (v1.2, 11/25/2024)

In this notebook, we calculate the superconductivity properties of MgB\(_2\) by solving the anisotropic Migdal-Eliashberg equations. The theory related to this tutorial can be found in Phys. Rev. B 87, 024505 (2013) which are also briefly discussed in this notebook.

Electrons and phonons are computed with Quantum ESPRESSO (QE), maximally-localized Wannier functions are computed with Wannier90, and superconductivity is computed with EPW. Using EPW, we do the following:

  1. We interpolate the electron-phonon matrix elements to fine k and q grids;

  2. Solve the Migdal-Eliashberg equations in the imaginary and real frequencies at different temperatures;

  3. We compared the solution of Migdal-Eliashberg equations with and without assuming the constant density of states.

NOTE: For this example, we use very coarse \(k\)- and \(q\)-grids. For actual calculations, one should use much denser grids.

Set up working environment#

[1]:

import numpy as np
import sys, os
sys.path.insert(0,str(os.getcwd())+'/../')
from EPWpy import EPWpy
from EPWpy.plotting import plot_supercond
pathQE='/home/shashi-phy/codes/q-e/bin'
print(pathQE)

/home/shashi-phy/codes/q-e/bin

Below we define constants that will remail unchanged throughout the Notebook. The object mgb2 is created as an instance of the EPWpy class. This object will contain everything that we need to execute and analyze the calculations.

Set paths to relevant directories:#

[2]:

prefix='mgb2'
pseudo='/home/shashi-phy/codes/epw_notebook/pseudos'
# Maximum number of cores to be used
cores = 8
print('Maximum number of cores to be used:', cores)

Maximum number of cores to be used: 8

Create Calculation Object#

Define general calculation parameters to be used throughout the workflow:

[3]:

mgb2=EPWpy.EPWpy({'prefix':prefix,
            'restart_mode':'\'from_scratch\'',
            'calculation':'\'scf\'',
            'ibrav':4,
            'nat':3,
            'ntyp':2,
            'atomic_species':['Mg', 'B'],
            'celldm(1)':'5.8260252227888',
            'celldm(3)':'1.1420694129095',
            'atoms':['Mg', 'B', 'B'],
            'atomic_pos':np.array([[0.0, 0.0, 0.0], [0.3333,0.66667,0.5],[0.66667,0.3333,0.5]]),
            'atomic_position_type':'crystal',
            'mass':[24.305, 10.811],
            'pseudo':['Mg.pz-n-vbc.UPF', 'B.pz-vbc.UPF'],
            'ecutwfc':'40',
            'ecutrho':'160',
            'smearing':'\'mp\'',
            'occupations':'\'smearing\'',
            'degauss':'0.05',
            'pseudo_dir':'\''+str(pseudo)+'\''},
            code=pathQE,
            env='mpirun',system = prefix)
#######Printing any attribute######
pseudopot=mgb2.__dict__['pw_atomic_species']['pseudo']
print('prefix:', mgb2.__dict__['pw_control']['prefix'])
print('pseudopotential:', mgb2.__dict__['pw_atomic_species']['pseudo'][0])
print('pseudopotential directory:', mgb2.__dict__['pw_control']['pseudo_dir'])




                                       -*#*-                             ...............-
                          .+*=      .+%*-=%%:      .=#*-               -===============-:.
                        :*%=*%%-    *%*   #%*    :+%+-%%+             .:.  -=.   :==-.
                        -%S  -%%*: :#%.   -%%-. -##:  #%*                  -=.   :==-
                ..      .%S:   +%%%%*.     :*%%%#=    %%=                  -=.   :==-
              :=#%%*-   .#S-     ..                  .%%=     :*#*:        -=.   :==-
             -%S:.=#%%*==%#                           *%%=::=##-+%%.  .   .=-.   :==-  .=
             :%%-   .-+++:                             -+##*=.  =%S   :-::==:    .==-  --.
              *%#                                               #%+    -=--:.     .----:.
              :%%-                                             -%S.
       .-=*####SS%#########:  -###########*+:     +#######=   =%SS####+::.
     =+#**%SSSSSSSSSSSSSSSS=  =SSSSSSSSSSSSSSS=   #SSSSSSS*.  +SSSSSSSS%%%%-
     *%%    =SSS..     .SSS=     SSS=.   .:+SSS+   -SSS:. .-::.  .SSS+.  #%*
      #%#.  =SSS.  *S#  *S%:     SSS=       %SS%.  .SSS=  #SSS%. :SSS:  =%#.
       *%%: =SSS#*#SSS-          SSS=     .+SSS+.   %SS*.=SSSSS+ +SS%.:+%+
        +%%:=SSSSSSSSS-          SSSSSSSSSSSSS=.    +SSS:SSS%SSS:%SS*-#%=
     ....#S==SSS:..SSS:  =+-     SSS%######+=.      -SSS%SS%.#SS%SSS==%%=.
 .:+##%%#*- =SSS.   ::. :SSS.    SSS=.               SSSSSS:..SSSSSS: :*%%%*=-
 #%+.     -+#SSS*+++++++*SSS: .=+SSS#++++:           %SSSS+.  =SSSS%.    :-+#%%+
 #%*     .SSSSSSSSSSSSSSSSSS: *SSSSSSSSSSS.          +SSS%.    %SSS*.      . .%%=
 =%S       :::::::::::::::::.  .:::::::::.            :::.      :::.     =+=-.#%+
 -%S:                                                                    =+===#S:
 ==*------------------------------=========+++++++++++++++++++++++========++-+##
 =+++++++++++*******++++++++++++++++========------------------==========+++++++-
-- -- -- -- -- -- -- -- -- -- -- -- Structure Info -- -- -- -- -- -- -- -- -- -- -- -- --
2
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
prefix: mgb2
pseudopotential: Mg.pz-n-vbc.UPF
pseudopotential directory: '/home/shashi-phy/codes/epw_notebook/pseudos'

Self-Consistent Field (SCF) Calculations#

We first solve the Kohn-Sham equations to obtain the Kohn-Sham orbitals \(\phi_v(r)\), where \(r\) is the electronic position (generally a mesh grid), and \(R\) is the position of ions.

\(E[\phi_v,R]=-\frac{\hbar^2}{2m}\sum_v{\int{\phi_v^\star(r)\nabla^2\phi_v(r)dr}+\int{V_R(r)n(r)dr}+\frac{e^2}{2}\int{\frac{n(r)n(r')}{|r-r'|}drdr'}+E_{xc}[n(r')]+\sum_{I\neq J}{\frac{e^2}{2}\frac{Z_IZ_J}{|R_I-R_J|}}}\)

We minimize \(E(R)=min(E[\phi_v,R])\)

Where, \(\Big(-\frac{\hbar^2}{2m}\nabla^2+V_{KS}(r)\Big)\phi_v(r)=\epsilon_v\phi_v(r)\)

[4]:

mgb2.scf(kpoints={'kpoints':[[8,8,8]],'type':'automatic'},name='scf')
mgb2.prepare(1,type_run='scf')
mgb2.run(cores, type_run='scf')

-- -- -- -- -- -- -- -- -- -- --  Calculation: scf  -- -- -- -- -- -- -- -- -- -- --
Running scf |████████████████████████████████████████| in 0.0s (4366.51/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Band Structure Calculation#

We now calculate the band structure of the material.

The band structure is the eigenenergies of KS orbitals at various points in the Brillouin zone. We choose a path that passes through all the high symmetry \(k\)-points.

\(\Big(-\frac{\hbar^2}{2m}|k+G|^2+V_{KS}(G-G')\Big)\phi_v(k)=\epsilon_v(k)\phi_v(k)\)

[5]:

mgb2.scf(control={'calculation':'\'bands\''},
         kpoints={'kpoints':[['0.0', '0.0', '0.0', '20'],
                            ['0.333', '0.333', '0.0', '20'],
                            ['0.5', '0.0', '0.0', '20'],
                            ['0.0', '0.0', '0.0', '20'],
                            ['0.0', '0.0', '0.5', '20'],
                            ['0.333', '0.333', '0.5', '20'],
                            ['0.5','0.0','0.5','20'],
                            ['0.0', '0.0', '0.5', '20']],
                  'kpoints_type':'{crystal_b}'},
            name='bs')

########################################
mgb2.prepare(1,type_run='bs')
mgb2.run(cores,type_run='bs')

-- -- -- -- -- -- -- -- -- -- --  Calculation: bs  -- -- -- -- -- -- -- -- -- -- --
Running bs |████████████████████████████████████████| in 0.0s (5391.53/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

[6]:

mgb2.bands(name='bands')
mgb2.prepare(1,type_run='bands')
# Running on too many cores will cause the job to fail
mgb2.run(cores,type_run='bands')

-- -- -- -- -- -- -- -- -- -- --  Calculation: bands  -- -- -- -- -- -- -- -- -- -- --
Running bands |████████████████████████████████████████| in 0.0s (4166.66/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Plotting band structure#

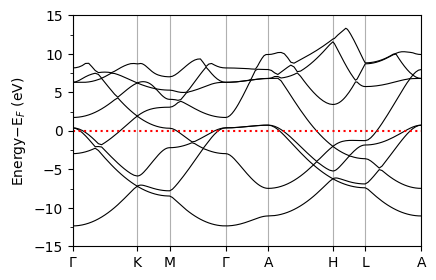
The band structure is given in the file bands.dat and plottable bands are written to bands.dat.gnu, which contains two columns The first column is the distance along the \(k\)‐path, and the second column is the energies (eV). We will use this file for plotting as below.

[4]:

ef = plot_supercond.get_fermi(prefix)
xticks=['$\Gamma$','K', 'M', '$\Gamma$', 'A', 'H', 'L', 'A']
plot_supercond.band_plot(prefix, xticks, ylim=(-15,15))

Plot saved as: mgb2_band.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_15_1.png

Density of states (DOS) calculation using tetrahedron method#

[6]:

mgb2.scf_fold='scf'
mgb2.scf(control={'calculation':'\'nscf\''},
        system={'occupations':'\'tetrahedra\''},
        kpoints={'kpoints':[[8,8,8]],
                'kpoints_type':'automatic'},
        name = 'nscf2')

mgb2.prepare(1, type_run='nscf2')
mgb2.run(cores, type_run='nscf2')

-- -- -- -- -- -- -- -- -- -- --  Calculation: nscf2  -- -- -- -- -- -- -- -- -- -- --
Running nscf2 |████████████████████████████████████████| in 0.0s (10021.23/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

[7]:

ef = plot_supercond.get_fermi(prefix)
mgb2.dos(dos={'prefix':prefix,
            'Emin':ef - 15,
            'Emax':ef + 15})
mgb2.prepare(1,type_run='dos')
mgb2.run(cores,type_run='dos')

-- -- -- -- -- -- -- -- -- -- --  Calculation: dos  -- -- -- -- -- -- -- -- -- -- --
Running dos |████████████████████████████████████████| in 0.0s (2422.14/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

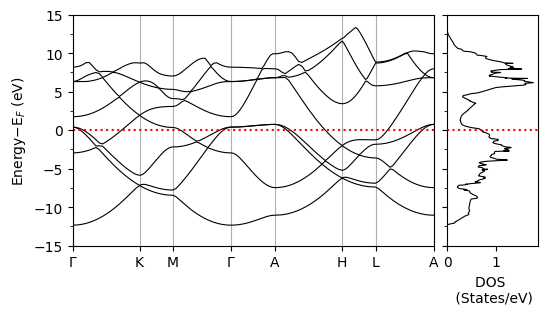
Plotting the Band Structure and DOS#

We now plot the band structure of the material.

[8]:

xticks=['$\Gamma$','K', 'M', '$\Gamma$', 'A', 'H', 'L', 'A']
plot_supercond.bandos_2plot(prefix, xticks)

Plot saved as: mgb2_band_dos.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_20_1.png

Phonon Calculations#

In order to obtain the Eliashberg spectral function, we need the electron-phonon interactions, which are the first derivatives of the lattice potential with respect to the atomic displacements. We also need the phonon frequencies and the displacement vectors. We obtain all these quantities using the density-functional perturbation theory (DFPT), as discussed in the tutorial.

We solve here using a \(3 \times 3 \times 3\) \(q\)-grid.

[9]:

mgb2.ph(phonons={'fildyn':'\'mgb2.dyn\'','nq1':3,'nq2':3,'nq3':3,'fildvscf':'\'dvscf\''})
mgb2.prepare(4,type_run='ph')
mgb2.run(cores,type_run='ph')

-- -- -- -- -- -- -- -- -- -- --  Calculation: ph  -- -- -- -- -- -- -- -- -- -- --
Running ph |████████████████████████████████████████| in 0.1s (2243.23/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Phonon Dispersion Calculation#

We begin by evaluating the interatomic force constants obtained via second derivatives of the total potential energy, \(C_{\kappa\alpha\rho\kappa'\alpha'\rho'}=\frac{\partial^{2}U}{\partial\tau_{\kappa\alpha\rho}\partial\tau_{\kappa'\alpha'\rho'}}\)

[9]:

mgb2.ph_fold='ph'
mgb2.q2r(name='q2r')
mgb2.prepare(1,type_run='q2r')
mgb2.run(4,type_run='q2r')

-- -- -- -- -- -- -- -- -- -- --  Calculation: q2r  -- -- -- -- -- -- -- -- -- -- --
Running q2r |████████████████████████████████████████| in 0.0s (5056.77/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

[10]:

mgb2.matdyn(matdyn={'flfrq':'\''+str(prefix)+'.freq\'',
                    'flfrc':str(prefix)+'.fc'},
            kpoints={'kpoints':[['0.0', '0.0', '0.0', '20'],
                            ['0.333', '0.333', '0.0', '20'],
                            ['0.5', '0.0', '0.0', '20'],
                            ['0.0', '0.0', '0.0', '20'],
                            ['0.0', '0.0', '0.5', '20'],
                            ['0.333', '0.333', '0.5', '20'],
                            ['0.5','0.0','0.5','20'],
                            ['0.0', '0.0', '0.5', '1']]},
            name='matdyn')

mgb2.prepare(1,type_run='matdyn')
mgb2.run(4,type_run='matdyn')

-- -- -- -- -- -- -- -- -- -- --  Calculation: matdyn  -- -- -- -- -- -- -- -- -- -- --
Running matdyn |████████████████████████████████████████| in 0.0s (7348.71/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Phonon DOS Calculation#

[11]:

mgb2.phdos(name='phdos',
          phdos={'flfrq':'\''+str(prefix)+'.dos.freq\'',
                  'flfrc':'\''+str(prefix)+'.fc\'',
                  'fldos':'\''+str(prefix)+'.dos\'',
                  'dos':'.true.',
                  'nk1':12,
                  'nk2':12,
                  'nk3':12,})
## Prepare folders and copy necessary files ##
mgb2.prepare(1,type_run='phdos')
## Run calculation ##
mgb2.run(cores,type_run='phdos')

-- -- -- -- -- -- -- -- -- -- --  Calculation: phdos  -- -- -- -- -- -- -- -- -- -- --
Running phdos |████████████████████████████████████████| in 0.0s (8388.52/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

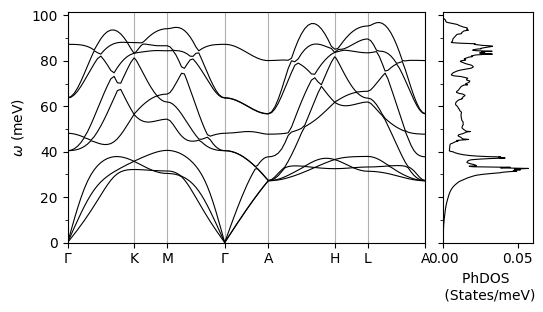
Plotting Phonon Dispersion and DOS#

[12]:

xticks=['$\Gamma$','K', 'M', '$\Gamma$', 'A', 'H', 'L', 'A']
plot_supercond.phonon_plot(prefix, xticks)

Plot saved as: mgb2_phonons.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_29_1.png

Transformation of electrons and phonons to Wannier basis with EPW#

Now we have Kohn-Sham wavefunctions and variations of the self-consistent Kohn-Sham potential on coarse Brillouin zone grid. We will generate the electron Hamiltonian, the IFCs, and the electron-phonon matrix elements in the Wannier representation using EPW. Details on the underlying formalism can be found here (free version) or here (journal version).

This operation involves four logical steps: 1. Compute Kohn-Sham states on a uniform \(\Gamma\) centered Brillouin zone grid (QE) between [0, 1] in crystal coordinates 2. Use EPW to load these states and call Wannier90 to generate Wannier functions 3. Use EPW to load IFCs (or dynamical matrices) and potential variations, and combine with step 2 to compute electron-phonon matrix elements in the Bloch representation 4. Use EPW to perform the transformation to the Wannier basis and write to file

Step 1: Calculations of Kohn-Sham states on uniform Brillouin zone grid#

We now perform a non-self-consistent DFT calculation on a homogeneous \(\Gamma\) centered \(k\)-point grid of \(6 \times 6 \times 6\).

[15]:

mgb2.nscf(control={'calculation':'\'bands\''},
          system={'nbnd':10,
                  'smearing':'\'mp\'',
                  'occupations':'\'smearing\'',
                  'degauss':'0.05',},
          kpoints={'grid':[6, 6, 6],'kpoints_type': 'crystal'})
mgb2.prepare(1, type_run='nscf')
######### Run #####################
mgb2.run(cores, type_run='nscf')

-- -- -- -- -- -- -- -- -- -- --  Calculation: nscf  -- -- -- -- -- -- -- -- -- -- --
Running nscf |████████████████████████████████████████| in 0.0s (5710.30/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Steps 2-4: Load Bloch representation, Wannierize, write to file quantities in Wannier representation#

Now, we have the phonon spectra, the dynamical matrix elements, and the electron-phonon interactions as discussed in the RMP paper. We interpolate dynamical matrix elements, and the electron-phonon coupling matrices using the EPW code.

[6]:

mgb2.ph_file='ph'
mgb2.ph_fold='ph'
mgb2.scf_fold='scf'
mgb2.nscf_file='nscf'
mgb2.nscf_fold='nscf'
mgb2.verbosity = 2
#kpath file
mgb2.filkf_file = 'mgb2.kpath.txt'

# EPW run 1: Bloch to Wannier
mgb2.epw(epwin={'wdata':['guiding_centres = .true.',
                       'dis_num_iter = 300',
                       'num_print_cycles  = 10',
                       'dis_mix_ratio = 1',
                       'use_ws_distance = T'],
                      'proj':['\'B:pz\'', '\'f=0.5,1.0,0.5:s\'', '\'f=0.0,0.5,0.5:s\'', '\'f=0.5,0.5,0.5:s\''],
                      'dis_froz_max':8.8,
                      'nbndsub':5,
                      'num_iter':500,
                      'etf_mem':0,
                      'elph':'.true.',
                      'band_plot':'.true.',
                      'filkf':mgb2.filkf_file,
                      'filqf':mgb2.filkf_file
                       },name='epw1')

mgb2.prepare(4, type_run='epw1')
mgb2.run(cores, type_run='epw1')

(4, 3)
[51, 51, 51]
User-provided filkf: mgb2.kpath.txt
-- -- -- -- -- -- -- -- -- -- --  Calculation: epw1  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 8 /home/shashi-phy/codes/q-e/bin/epw.x -nk 8 -in  epw1.in > epw1.out
Running epw1 |████████████████████████████████████████| in 0.0s (3753.06/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

At this point, we have all necessary quantities in the Wannier representation on file. As a sanity check, we perform a simple interpolation of bands and phonons to make sure that we reproduce the results found above without Wannier interpolation.

[7]:

#electron eigen energies
mgb2.plotband(name='plotband')
mgb2.prepare(1,type_run='plotband')
mgb2.run(1,type_run='plotband')

-- -- -- -- -- -- -- -- -- -- --  Calculation: plotband  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 1 /home/shashi-phy/codes/q-e/bin/plotband.x <  plotband.in > plotband.out
Running plotband |████████████████████████████████████████| in 0.0s (2975.62/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

[8]:

#ef = plot_supercond.get_fermi(prefix)
xticks=['$\Gamma$','K', 'M', '$\Gamma$', 'A', 'H', 'L', 'A']
sym_file = './mgb2/epw/plotband.out'
band_file = './mgb2/epw/band.dat'
plot_supercond.band_plot(prefix, xticks, band_file=band_file, sym_file=sym_file)

Plot saved as: mgb2_band.pdf
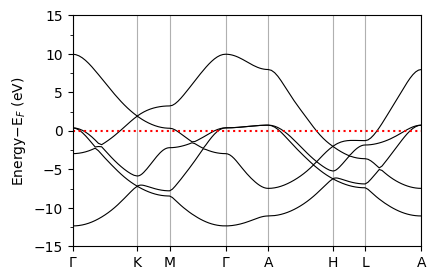
../../_images/doc_notebooks_supercond_aniso_v1.2_37_1.png

Interpolation of phonon frequencies#

[9]:

#Generate phonon interpolated band
mgb2.plotband(['phband.freq',
             '0 100', # frequncy range
             'phband.dat']
            ,name='plotband')
mgb2.prepare(1, type_run='plotband')
mgb2.run(1, type_run='plotband')

-- -- -- -- -- -- -- -- -- -- --  Calculation: plotband  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 1 /home/shashi-phy/codes/q-e/bin/plotband.x <  plotband.in > plotband.out
Running plotband |████████████████████████████████████████| in 0.0s (3900.05/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

[10]:

xticks=['$\Gamma$','K', 'M', '$\Gamma$', 'A', 'H', 'L', 'A']

#EPW interpolated band
plot_supercond.phband_plot(prefix, xticks, band_file='./mgb2/epw/phband.dat',sym_file='./mgb2/epw/plotband.out')

#QE phonon band
plot_supercond.phband_plot(prefix, xticks, band_file='./mgb2/ph/mgb2.freq.gp',sym_file='./mgb2/bs/bands.out')

Reading data from: ./mgb2/epw/phband.dat
Plot saved as: mgb2_phonon_dispersion.pdf
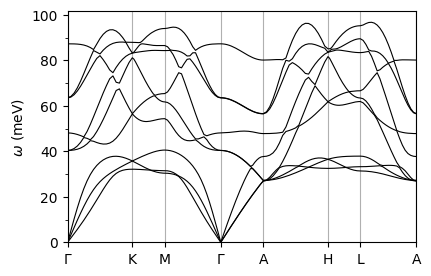
../../_images/doc_notebooks_supercond_aniso_v1.2_40_1.png 
Reading data from: ./mgb2/ph/mgb2.freq.gp
Plot saved as: mgb2_phonon_dispersion.pdf
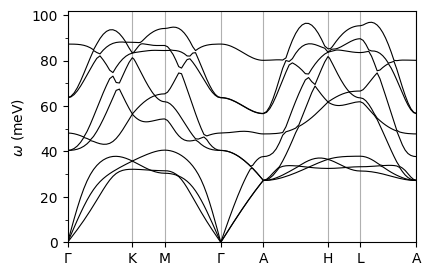
../../_images/doc_notebooks_supercond_aniso_v1.2_40_3.png

Superconductivity Calculations#

The theory related to this tutorial can be found in Phys. Rev. B 87, 024505 (2013). Below we briefly discuss the theory.

The adiabatic self-energy can be written as:

\[\Sigma_{nk}(i\omega_j) = -T \sum_{mk'}\sum_{j'} \sum_{\nu} |g_{nk,mk'}^{-q\nu}|^2 D^0_{q\nu}(i\omega_j-i\omega_{j'})\tau_{3}\Sigma_{mk'}(i\omega_{j'}) \tau_{3}\]

where the dressed phonon propagator is expressed in terms of its spectral representation as

\[D^0_{q\nu}(i\omega_j-i\omega_{j'}) = -\frac{2\omega_{q\nu}}{(\omega_j-\omega_{j'})^2 + \omega_{q\nu}^2} = \frac{2\omega_{q\nu}}{(i\omega_j-i\omega_{j'})^2 - \omega_{q\nu}^2}\]

The anisotropic electron-phonon coupling strength is defined as follows,

\[\lambda_{nk, mk+q}(\omega_j) = N_F \sum_{\nu} \frac{2\omega_{q\nu}}{\omega_j^2 + \omega_{q\nu}^2} \left|g_{nk,mk'}^{-q\nu}\right|^2 = \int_{0}^{\infty} d\omega \frac{2\omega}{\omega_j^2 + \omega^2} \alpha^2F_{nk,mk+q}(\omega)\]

where \(N_F\) is the density of states at the Fermi energy.

The band- and wavevector-dependent electron-phonon coupling strength \(\lambda_{nk}(\omega_j)\) is defined as:

\[\lambda_{nk}(\omega_j) = \sum_{m} \int \frac{dq} {\Omega_{\rm BZ}} \frac{\delta(\varepsilon_{mk+q}-\varepsilon_F)}{N_F} \lambda_{nk, mk+q}(\omega_j)\]

The isotropic electron-phonon coupling strength takes the following form

\[\lambda(\omega_j) = \sum_{n} \int \frac{dk}{\Omega_{\rm BZ}}\frac{\delta(\varepsilon_{nk}-\varepsilon_F)}{N_F} \lambda_{nk}(\omega_j)\]

The standard electron-phonon coupling strength \(\lambda\) found in the literature corresponds to setting \(\omega_j=0\) in the isotropic electron-phonon coupling strength.

The anisotropic Eliashberg spectral functions is defined as

\[\alpha^2F_{nk,mk+q}(\omega) = N_F \sum_{\nu} \left|g_{nk,mk'}^{-q\nu}\right|^2 \delta(\omega-\omega_{q\nu})\]

To compare with available experimental data, we define the Fermi-surface averaged spectral functions as follows (see EPW paper).

\[\alpha^2F(\omega) = \frac{1}{N_F} \sum_{nm\nu} \int \frac{dk} {\Omega_{\rm BZ}} \int \frac{dq} {\Omega_{\rm BZ}} \left|g_{nk,mk'}^{-q\nu}\right|^2 \delta(\omega-\omega_{q\nu}) \delta(\varepsilon_{nk}-\varepsilon_F) \delta(\varepsilon_{mk+q}-\varepsilon_F)\]

From several studies, it was observed that \(\alpha^2F(\omega)\) closely resembles the phonon density of states :math:`F(omega) <https://www.sciencedirect.com/science/article/pii/S0081194708606657>`__.

Fermi-Surface Restricted (FSR) Migdal-Eliashberg Equations#

Following the procedure as discussed in this paper, we solve the anisotropic FSR Migdal-Eliashberg equations on the imaginary frequency axis by setting the keywords eliashberg = .true., laniso = .true., and limag = .true. in the EPW input file. The equations are solved self-consistently for each temperature specified in temps in the input file. The calculation at each temperature ends when either the converge threshold (set with conv_thr_iaxis) or the maximum number of iterations (set with nsiter) is reached.

The anisotropic FSR Migdal-Eliashberg equations take the following form:

\[Z_{nk}(i\omega_j)= 1 + \frac{\pi T}{\omega_j N_F} \sum_{mj'}\int \frac{dq}{\Omega_{\rm BZ}}\frac{\omega_{j'}}{\sqrt{\omega_{j'}^2 + \Delta_{mk+q}^2}} \lambda_{nk,mk+q}(\omega_j - \omega_{j'}) \delta(\varepsilon_{mk+q}-\varepsilon_F)\]

and

\[Z_{nk}(i\omega_j) \Delta_{nk}(i\omega_j) = \frac{\pi T}{N_F} \sum_{m{j'}} \int \frac{dq} {\Omega_{\rm BZ}} \frac{\Delta_{mk+q}}{\sqrt{\omega_{j'}^2 + \Delta_{mk+q}^2}} \left[\lambda_{nk,mk+q}(\omega_j - \omega_{j'}) -\mu_c^*\right] \delta(\varepsilon_{mk+q}-\varepsilon_F)\]

where \(\lambda_{nk,mk+q}(\omega_j- \omega_{j'})\) is the anisotropic electron-phonon coupling strength. The semiempirical Coulomb parameter \(\mu_c^*\) is provided as an input varible muc in the EPW calculation.

From these expressions, we observe that the necessary ingredients to solve the anisotropic ME equations are the Kohn-Sham eigenvalues, phonon frequencies, and electron-phonon matrix elements on the \(k\)- and \(q\)-grids.

Once electron-phonon matrix elements on denser \(k\)- and \(q\)-grids are computed, we will then solve the Eliashberg equations self-consistently to obtain the ansitropic gap function. To understand the gap function, we will also analyze the electron-phonon coupling \(\lambda\).

To compute the superconducting properties, we perform the following operations: 1. Fourier-transform the electron-phonon matrix elements and interpolate from a coarse \(k\)-grid of \(6\times 6 \times 6\) and \(q\)-grid of \(3 \times 3 \times 3\) to dense \(20 \times 20 \times 20\) \(k\)-point and \(10 \times 10 \times 10\) \(q\)-point grids, respectively.

- Pre-compute the $q$-points that fall within the Fermi window `fsthick`. If, at a specific $q$-point, at least one $k+q$ eigen energy falls within `fsthick` of the Fermi level, then the $q$-point is selected.
- For superconductivity calculations, we must set `ephwrite = .true.`. This also requires  that the $k$- and $q$-grids be commensurate, i.e., `nkf1`, `nkf2`, `nkf3` to be integer multiples of `nqf1`, `nqf2`, `nqf3`, respectively.

  1. We use the interpolated e-ph couplings to solve the Eliashberg expressions as discussed above.

    • Write the Fermi surface files mgb2.fs\_YY.cube (YY = band index within the fsthick) and mgb2.fs.frmsf by setting fermi_plot = .true.. The *.cube files can be visualized with VESTA and the *.frmsf file can be visualized with FermiSurfer.

    • Calculate the isotropic and anisotropic electron-phonon coupling strength by setting the keywords eliashberg = .true. and iverbosity = 2. The expressions for isotropic and anisotropic electron-phonon coupling strengths are given above.

    • Solve the anisotropic Migdal-Eliashberg equations on the imaginary frequency axis achieved by setting the keywords laniso = .true., and limag = .true. in the input file. The equations are solved self-consistently for each temperature specified in the input file. The calculation at each temperature ends when either the converge threshold or the maximum number of iterations is reached.

    • Perform the analytic continuation of the solutions along the imaginary frequency axis to the real frequency axis by using Pade approximants (from lpade=.true.). Note the analytic continuation with the iterative procedure (from lacon = .true.) is not performed since this is very expensive computationally in the anisotropic case (hours to days).

[11]:

mgb2.epw(epwin={ 'elph':'.true.',
                 'fsthick':0.2,
                 'degaussw':0.05,
                 'degaussq':0.5, #phonon smearing
                 'ephwrite':'.true.',
                 'eliashberg':'.true.',
                 'iverbosity':2,
                 'laniso':'.true.',
                 'limag':'.true.',
                 'lpade':'.true.',
                 'nsiter': '500',
                 'conv_thr_iaxis':'1.0d-3',
                 'wscut' :'0.5', # maximum matsubara freq. cutoff
                 'muc':'0.1',
                 'nstemp':'4',
                 'temps':'10 30',
                 'nkf1':20,'nkf2':20,'nkf3':20,
                 'nqf1':10,'nqf2':10,'nqf3':10,
                 'mp_mesh_k':'.true.', # uses k-point symmetry
                 'clean_supercond':None},
         name='epw2')

mgb2.prepare(4,type_run='epw2')
mgb2.run(cores,type_run='epw2')

-- -- -- -- -- -- -- -- -- -- --  Calculation: epw2  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 8 /home/shashi-phy/codes/q-e/bin/epw.x -nk 8 -in  epw2.in > epw2.out
Running epw2 |████████████████████████████████████████| in 0.0s (3139.89/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Plotting the Isotropic and Anisotropic Electron-Phonon Coupling Strengths#

-The files mgb2.lambda_pairs, mgb2.lambda_k_pairs, and mgb2.a2f are generated by setting eliashberg = .true. and iverbosity = 2.

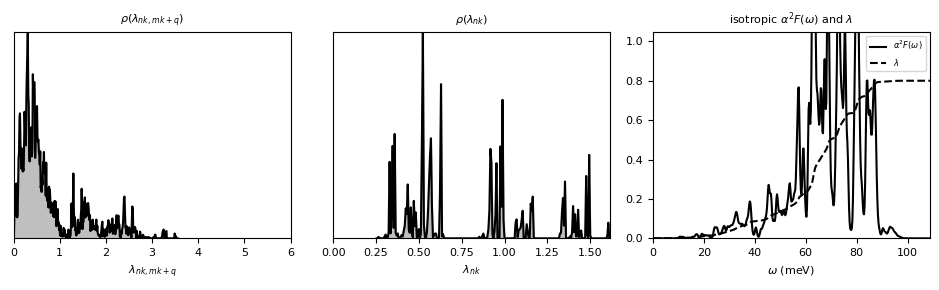
-The mgb2.lambda_pairs file contains the anisotropic electron-phonon coupling strength \(\lambda_{nq,mk+q}(0)\) on the Fermi surface.

-The mgb2.lambda_k_pairs file contains the band- and wavevector-dependent anisotropic electron-phonon coupling strength \(\lambda_{nk}(0)\) on the Fermi surface.

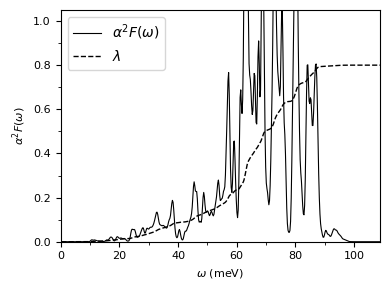
-The mgb2.a2f file contains the isotropic Eliashberg spectral function \(\alpha^2F(\omega)\) and cumulative electron-phonon coupling strength as a function of frequency \(\omega\)(meV) for different phonon smearing values (see the end of the file for information about the smearing).

[12]:

###Anisotropic electron-phonon coupling
lambda_pairs = "./mgb2/epw/mgb2.lambda_pairs"
lambda_k_pairs = "./mgb2/epw/mgb2.lambda_k_pairs"
plot_supercond.plot_lambda(prefix, lambda_pairs_file=lambda_pairs, lambda_k_pairs_file=lambda_k_pairs)
#plot_supercond.plot_lambda(prefix, font=10)

Plot saved as: ./mgb2_lambda_pairs.pdf
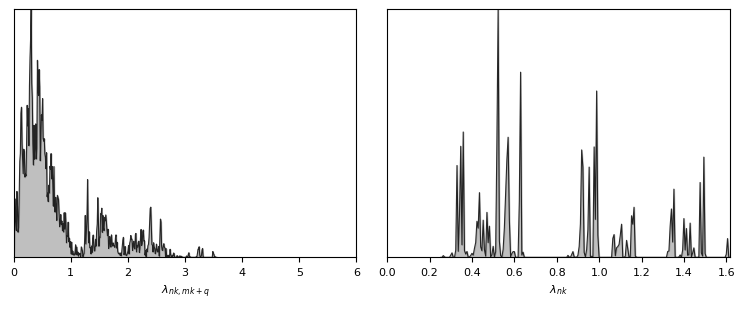
../../_images/doc_notebooks_supercond_aniso_v1.2_46_1.png 
[13]:

###Isotropic a2f and electron-phonon coupling
plot_supercond.plot_a2f(prefix)

Plot saved as: mgb2_a2f_plot.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_47_1.png 
[14]:

###Ansiotropic and isotropic electron-phonon coupling
plot_supercond.plot_lambda_aniso_iso(prefix)

Plot saved as: ./mgb2_aniso_iso_e-ph_coupling.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_48_1.png 
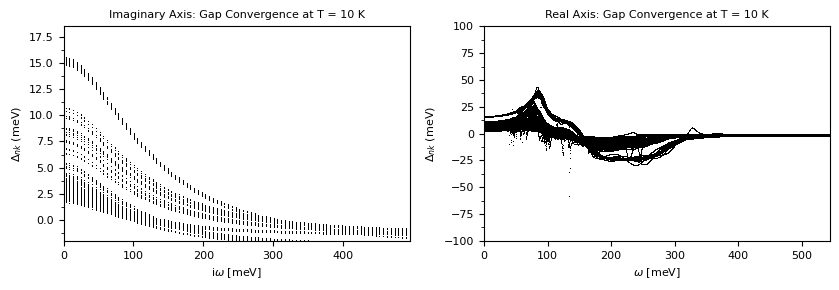
[15]:

plot_supercond.gap_conv_aniso_real_imag(prefix, temp=10)

Plot saved as: ./mgb2_gap_conv_Re_Im_axes.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_50_1.png 
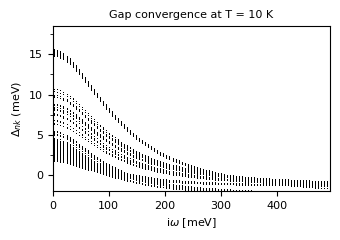
[16]:

#plot_supercond.gap_conv_aniso_imag(prefix, temp=10)
imag_gap = "mgb2/epw/mgb2.imag_aniso_010.00"
plot_supercond.gap_conv_aniso_imag(prefix, temp=10, imag_gap_files=imag_gap)

Plot saved as: ./mgb2_aniso_Im_gap_conv.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_51_1.png 
[17]:

plot_supercond.gap_aniso_temp(prefix, tempmax=35, font=8)

Plot saved as: /home/shashi-phy/codes/epw_notebook/notebooks_basic/mgb2_gap_aniso_vs_temp.pdf
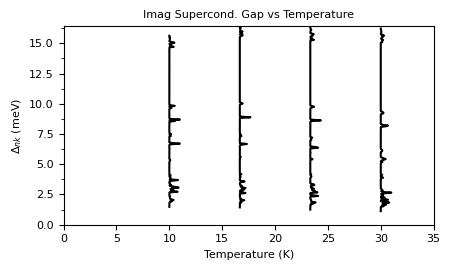
../../_images/doc_notebooks_supercond_aniso_v1.2_53_1.png

Superconducting Quasiparticle DOS#

The quasiparticle DOS in the superconducting state relative to the DOS in the normal state is given by:

\[\frac{N_S(\omega)}{N_F} = \sum_{n} \int \frac{dk} {\Omega_{\rm BZ}} \frac{\delta(\varepsilon_{nk}-\varepsilon_{F})}{N_F} {\rm Re} \left[ \omega/\sqrt{\omega^2 - \Delta_{nk}(\omega)} \right]\]

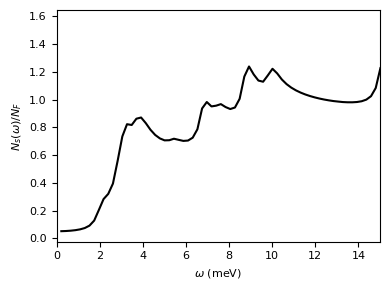
The mgb2.qdos_XX files contain the quasiparticle density of states in the superconducting state relative to the DOS in the normal state \(N_S(\omega)/N_F\) as a function of frequency (eV) at various temperatures.

[18]:

#plot_supercond.plot_qpdos(prefix, filename ='epw1.out', temp=10)
qdos = 'mgb2/epw/mgb2.qdos_010.00'
dos = 'mgb2/epw/epw2.out'
plot_supercond.plot_qpdos(prefix, qdos_file=qdos, dos_file=dos, temp=10)

Plot saved as: ./mgb2_Qpdos_10.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_56_1.png

Full-Bandwidth (FBW) Migdal-Eliashberg Equations#

We can solve the anisotropic self-energy expressions by considering the energy range within the fsthick window instead of using a constant density of states approximations as discussed in EPW-2023 paper.

\[{Z}_{n{{{\bf{k}}}}}(i{\omega }_{j})=1+\frac{{k}_{{{{\rm{B}}}}}T}{{\omega }_{j}N({\varepsilon }_{{{{\rm{F}}}}})}\mathop{\sum}\limits_{m{j}^{{\prime} }}\int\,\frac{{\rm {d}}{{{\bf{q}}}}}{{{{\Omega }}}_{{{{\rm{BZ}}}}}}\,\frac{{\omega }_{{j}^{{\prime} }}{Z}_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}{{\theta }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}\lambda (n{{{\bf{k}}}},m{{{\bf{k}}}}+{{{\bf{q}}}},{\omega }_{j}-{\omega }_{{j}^{{\prime} }}),\]
\[{\chi}_{n{{{\bf{k}}}}}(i{\omega }_{j})=-\frac{{k}_{{{{\rm{B}}}}}T}{N({\varepsilon }_{{{{\rm{F}}}}})}\mathop{\sum}\limits_{m{j}^{{\prime} }}\int\,\frac{{\rm {d}}{{{\bf{q}}}}}{{{{\Omega }}}_{{{{\rm{BZ}}}}}}\,\frac{{\varepsilon }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}-{\mu }_{{{{\rm{F}}}}}+{\chi }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}{{\theta }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}\lambda (n{{{\bf{k}}}},m{{{\bf{k}}}}+{{{\bf{q}}}},{\omega }_{j}-{\omega }_{{j}^{{\prime} }}),\]
\[{\phi }_{n{{{\bf{k}}}}}(i{\omega }_{j})=\frac{{k}_{{{{\rm{B}}}}}T}{N({\varepsilon }_{{{{\rm{F}}}}})}\mathop{\sum}\limits_{m{j}^{{\prime} }}\int\,\frac{{\rm {d}}{{{\bf{q}}}}}{{{{\Omega }}}_{{{{\rm{BZ}}}}}}\,\frac{{\phi }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}{{\theta }_{m{{{\bf{k}}}}+{{{\bf{q}}}}}(i{\omega }_{{j}^{{\prime} }})}\left[\lambda (n{{{\bf{k}}}},m{{{\bf{k}}}}+{{{\bf{q}}}},{\omega }_{j}-{\omega }_{{j}^{{\prime} }})-N({\varepsilon }_{{{{\rm{F}}}}}){V}_{n{{{\bf{k}}}},m{{{\bf{k}}}}+{{{\bf{q}}}}}\right]\]

where

\[{\theta }_{n{{{\bf{k}}}}}(i{\omega }_{j})={\left[\hslash {\omega }_{j}{Z}_{n{{{\bf{k}}}}}(i{\omega }_{j})\right]}^{2}+{\left[{\varepsilon }_{n{{{\bf{k}}}}}-{\mu }_{{{{\rm{F}}}}}+{\chi }_{n{{{\bf{k}}}}}(i{\omega }_{j})\right]}^{2}+{\left[{\phi }_{n{{{\bf{k}}}}}(i{\omega }_{j})\right]}^{2}.\]

The superconducting gap is defined in terms of the renormalization function and the order parameter as: \(\Delta_{nk} = \phi_{nk}(i\omega_j) / {Z_{nk}}\).

This set of equations is supplemented with an equation for the electron number \(N_\rm{e}\), which determines the chemical potential \(\mu_F\) if muchem = .true. is set in the EPW calculation.

\[{N}_{{{{\rm{e}}}}}=\mathop{\sum}\limits_{n}\int\frac{{\rm {d}}{{{\bf{k}}}}}{{{{\Omega }}}_{{{{\rm{BZ}}}}}}\left[1-2{k}_{{{{\rm{B}}}}}T\mathop{\sum}\limits_{j}\frac{{\varepsilon }_{n{{{\bf{k}}}}}-{\mu }_{{{{\rm{F}}}}}+{\chi }_{n{{{\bf{k}}}}}(i{\omega }_{j})}{{\theta }_{n{{{\bf{k}}}}}(i{\omega }_{j})}\right],\]

Here, \(N_\rm{e}\) is the number of electrons per unit cell.

In FBW calculations, use the tag fbw=.true. We can either keep the chemical potential constant or vary the chemical potential using the input tag muchem=.true..

[20]:

#mgb2.nscf_file='scf'
#mgb2.scf_fold='scf'
#mgb2.nscf_file='nscf'
#mgb2.nscf_fold='nscf'
#mgb2.ph_file='ph'
#mgb2.ph_fold='ph'
#mgb2.epw_fold='epw'

mgb2.epw(epwin={ 'elph':'.true.',
                 'fsthick':0.2,
                 'degaussw':0.05,
                 'degaussq':0.5, #phonon smearing
                 'ephwrite':'.true.',
                 'eliashberg':'.true.',
                 'iverbosity':2,
                 #'fermi_plot':'.true.',
                 'laniso':'.true.',
                 'limag':'.true.',
                 'fbw':'.true.',
                 'lpade':'.true.',
                 'nsiter': '500',
                 'conv_thr_iaxis':'1.0d-3',
                 'wscut' :'0.5', # maximum matsubara freq. cutoff
                 'muc':'0.1',
                 'nstemp':'4',
                 'temps':'10 30',
                 'nkf1':20,'nkf2':20,'nkf3':20,
                 'nqf1':10,'nqf2':10,'nqf3':10,
                 'mp_mesh_k':'.true.', # uses k-point symmetry
                 'clean_supercond':None},
         name='epw3')

mgb2.prepare(4, type_run='epw3')
mgb2.run(cores, type_run='epw3')

-- -- -- -- -- -- -- -- -- -- -- -- -- Warning -- -- -- -- -- -- -- -- -- -- -- -- -- --
Refreshing EPW input (remove refresh from epw_save.json if not needed)
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
-- -- -- -- -- -- -- -- -- -- --  Calculation: epw3  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 8 /home/shashi-phy/codes/q-e/bin/epw.x -nk 8 -in  epw3.in > epw3.out
Running epw3 |████████████████████████████████████████| in 0.0s (4809.80/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

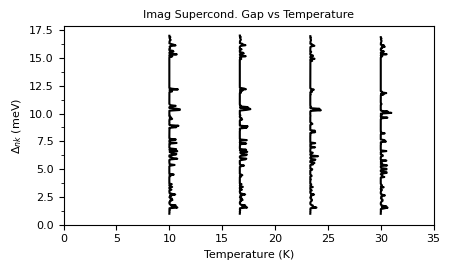
[21]:

plot_supercond.gap_aniso_temp(prefix, tempmax=35)

Plot saved as: /home/shashi-phy/codes/epw_notebook/notebooks_basic/mgb2_gap_aniso_vs_temp.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_59_1.png 
[22]:

mgb2.epw(epwin={ 'elph':'.true.',
                 'fsthick':0.2,
                 'degaussw':0.05,
                 'degaussq':0.5, #phonon smearing
                 'ephwrite':'.true.',
                 'eliashberg':'.true.',
                 'iverbosity':2,
                 #'fermi_plot':'.true.',
                 'laniso':'.true.',
                 'limag':'.true.',
                 'fbw':'.true.',
                 'muchem':'.true.',
                 'lpade':'.true.',
                 'nsiter': '500',
                 'conv_thr_iaxis':'1.0d-3',
                 'wscut' :'0.5', # maximum matsubara freq. cutoff
                 'muc':'0.1',
                 'nstemp':'4',
                 'temps':'10 30',
                 'nkf1':20,'nkf2':20,'nkf3':20,
                 'nqf1':10,'nqf2':10,'nqf3':10,
                 'mp_mesh_k':'.true.', # uses k-point symmetry
                 'clean_supercond':None},
         name='epw3')

mgb2.prepare(4, type_run='epw3')
mgb2.run(cores, type_run='epw3')

-- -- -- -- -- -- -- -- -- -- -- -- -- Warning -- -- -- -- -- -- -- -- -- -- -- -- -- --
Refreshing EPW input (remove refresh from epw_save.json if not needed)
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
-- -- -- -- -- -- -- -- -- -- --  Calculation: epw3  -- -- -- -- -- -- -- -- -- -- --
on 1: running:  mpirun -np 8 /home/shashi-phy/codes/q-e/bin/epw.x -nk 8 -in  epw3.in > epw3.out
Running epw3 |████████████████████████████████████████| in 0.0s (3047.37/s)

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

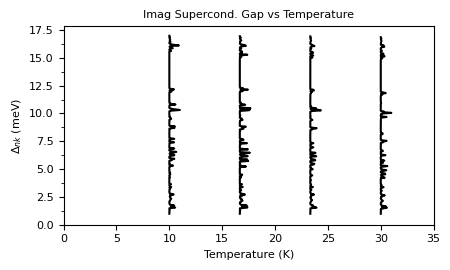
[23]:

plot_supercond.gap_aniso_temp(prefix, tempmax=35)

Plot saved as: /home/shashi-phy/codes/epw_notebook/notebooks_basic/mgb2_gap_aniso_vs_temp.pdf
../../_images/doc_notebooks_supercond_aniso_v1.2_62_1.png

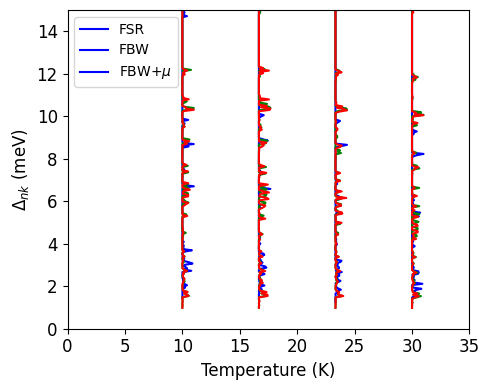
NOTE: If you want to make a plot to compare the superconducting gap using FSR, FBW and FBW+\(\mu\) type of calculations, after performing FBW and FBW+\(\mu\) calculations, move the mgb2.imag_aniso_gap0 to folders named as fbw and fbw_mu as the files are overwritten while running each type of calculations.

[7]:

plot_supercond.gap_aniso_fsr_fbw_mu_temp(prefix, tempmax=35, font=12)
../../_images/doc_notebooks_supercond_aniso_v1.2_64_0.png